No CrossRef data available.
Article contents
Combinatorially Factorizable Cryptic Inverse Semigroups
Published online by Cambridge University Press: 20 November 2018
Abstract
An inverse semigroup  $S$ is combinatorially factorizable if
$S$ is combinatorially factorizable if 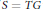 $S\,=\,TG$ where
$S\,=\,TG$ where 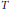 $T$ is a combinatorial (i.e.,
$T$ is a combinatorial (i.e., 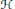 $\mathcal{H}$ is the equality relation) inverse subsemigroup of
$\mathcal{H}$ is the equality relation) inverse subsemigroup of  $S$ and
$S$ and 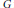 $G$ is a subgroup of
$G$ is a subgroup of  $S$. This concept was introduced and studied by Mills, especially in the case when
$S$. This concept was introduced and studied by Mills, especially in the case when  $S$ is cryptic (i.e.,
$S$ is cryptic (i.e., 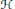 $\mathcal{H}$ is a congruence on
$\mathcal{H}$ is a congruence on  $S$). Her approach is mainly analytical considering subsemigroups of a cryptic inverse semigroup.
$S$). Her approach is mainly analytical considering subsemigroups of a cryptic inverse semigroup.
We start with a combinatorial inverse monoid and a factorizable Clifford monoid and from an action of the former on the latter construct the semigroups in the title. As a special case, we consider semigroups that are direct products of a combinatorial inverse monoid and a group.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2014




