Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-17T10:04:01.952Z Has data issue: false hasContentIssue false
  • English
  • Français

Fundamental Solutions of Kohn Sub-Laplacians on Anisotropic Heisenberg Groups and H-type Groups

Published online by Cambridge University Press:  20 November 2018

Yongyang Jin  and
Genkai Zhang
Yongyang Jin
Affiliation:
Department of Applied Mathematics, Zhejiang University of Technology, Hangzhou, 310032, Chinae-mail: yongyang@zjut.edu.cn
Genkai Zhang
Affiliation:
Department of Mathematics, Chalmers University of Technology and Göteborg University, Göteborg, Swedene-mail: genkai@chalmers.se
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that the fundamental solutions of Kohn sub-Laplacians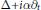$\Delta +i\alpha {{\partial }_{t}}$ on the anisotropic Heisenberg groups are tempered distributions and have meromorphic continuation in α with simple poles. We compute the residues and find the partial fundamental solutions at the poles. We also find formulas for the fundamental solutions for some matrix-valued Kohn type sub-Laplacians on 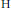$\text{H}$-type groups.

Keywords

22E3035R0343A80
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 126 - 140
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Beals, R., Gaveau, B., and Greiner, P., The Green function of model step two hypoelliptic operators and the analysis of certain tangential Cauchy Riemann complexes. Adv. Math. 121(1996), no. 2, 288–345. doi:10.1006/aima.1996.0054Google Scholar
[2] Calin, O., Chang, D.-C., and Tie, J., Fundamental solutions for Hermite and subelliptic operators. J. Anal. Math. 100(2006), 223–248. doi:10.1007/BF02916762Google Scholar
[3] Chang, D.-C. and Tie, J. Z., A note on Hermite and subelliptic operators. Acta Math. Sin. (Engl. Ser.) 21(2005), no. 4, 803–818. doi:10.1007/s10114-004-0336-0Google Scholar
[4] Cowling, M., Dooley, A., Korányi, A., and Ricci, F., An approach to symmetric spaces of rank one via groups of Heisenberg type. J. Geom. Anal. 8(1998), no. 2, 199–237.Google Scholar
[5] Cowling, M., Dooley, A., Korányi, A., and Ricci, F., H-type groups and Iwasawa decompositions. Adv. Math. 87(1991), no. 1, 1–41. doi:10.1016/0001-8708(91)90060-KGoogle Scholar
[6] Folland, G. B., A fundamental solution for a subelliptic operator. Bull. Amer. Math. Soc. 79(1973), 373–376. doi:10.1090/S0002-9904-1973-13171-4Google Scholar
[7] Heinonen, J. and Holopainen, I., Quasiregular maps on Carnot groups. J. Geom. Anal. 7(1997), no. 1, 109–148.Google Scholar
[8] Kaplan, A., Fundamental solutions for a class of hypoelliptic PDE generated by composition of quadratic forms. Trans. Amer. Math. Soc. 258(1980), no. 1, 147–153. doi:10.2307/1998286Google Scholar
[9] Nagel, A., Stein, E. M., and Wainger, S., Balls and metrics defined by vector fields. I. Basic properties. Acta Math. 155(1985), no. 1–2, 103–147. doi:10.1007/BF02392539Google Scholar
[10] Stein, E. M., Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals. Princeton Mathematical Series, 43, Monographs in Harmonic Analysis, III, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[11] Stein, E. M. and Weiss, G., Introduction to Fourier analysis on Euclidean spaces. Princeton Mathematical Series, 32, Princeton University Press, Princeton, NJ, 1971.Google Scholar
[12] Strichartz, R. S., Lp harmonic analysis and Radon transforms on the Heisenberg group. J. Funct. Anal. 96(1991), no. 2, 350–406. doi:10.1016/0022-1236(91)90066-EGoogle Scholar
[13] Thangavelu, S., Lectures on Hermite and Laguerre expansions. Mathematical Notes, 42, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[14] Whittaker, E. T. and Watson, G. N., A course of modern analysis. An introduction to the general theory of infinite processes and of analytic functions: with an account of the principal transcendental functions. Fourth ed., Reprinted Cambridge University Press, New York, 1962.Google Scholar