Let $G$ be a compact topological group and let 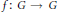$f:\,G\,\to \,G$ be a continuous transformation of $G$. Define 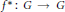${{f}^{*}}:G\to G$ by 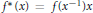${{f}^{*}}\left( x \right)\,=\,f\left( {{x}^{-1}} \right)x$ and let 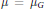$\mu \,=\,{{\mu }_{G}}$ be Haar measure on $G$. Assume that 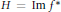$H\,=\,\text{IM}\,{{f}^{*}}$ is a subgroup of $G$ and for every measurable 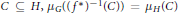$C\,\subseteq \,H,\,{{\mu }_{G}}{{\left( \left( {{f}^{*}} \right) \right)}^{-1}}\left( \left( C \right) \right)\,=\,\mu H\left( C \right)$. Then for every measurable $C\,\subseteq \,G$, there exist 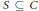$S\subseteq C$ and 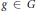$g\,\in \,G$ such that 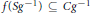$f\left( S{{g}^{-1}} \right)\,\subseteq \,C{{g}^{-1}}$ and 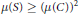$\mu \left( S \right)\,\ge \,{{\left( \mu \left( C \right) \right)}^{2}}$.