Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-19T13:06:53.065Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise Convergence of Solutions to the Schrödinger Equation on Manifolds

Part of: Harmonic analysis in several variables Hyperbolic equations and systems Linear function spaces and their duals

Published online by Cambridge University Press:  07 January 2019

Xing Wang  and
Chunjie Zhang
Xing Wang
Affiliation:
Department of Mathematics, Wayne State University, Detroit, Michigan 48202, USA Email: xing.wang@wayne.edu
Chunjie Zhang*
Affiliation:
Department of Mathematics, Hangzhou Dianzi University, MHangzhou, 310018, China Email: purezhang@hdu.edu.cn
*
*Chunjie Zhang is the corresponding author.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 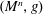$(M^{n},g)$ be a Riemannian manifold without boundary. We study the amount of initial regularity required so that the solution to a free Schrödinger equation converges pointwise to its initial data. Assume the initial data is in 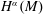$H^{\unicode[STIX]{x1D6FC}}(M)$. For hyperbolic space, the standard sphere, and the two-dimensional torus, we prove that 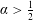$\unicode[STIX]{x1D6FC}>\frac{1}{2}$ is enough. For general compact manifolds, due to the lack of a local smoothing effect, it is hard to improve on the bound 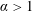$\unicode[STIX]{x1D6FC}>1$ from interpolation. We managed to go below 1 for dimension 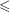${\leqslant}$ 3. The more interesting thing is that, for a one-dimensional compact manifold, 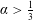$\unicode[STIX]{x1D6FC}>\frac{1}{3}$ is sufficient.

Keywords

pointwise convergenceSchrödinger operatormanifoldStrichartz estimate

MSC classification

Primary: 35L05: Wave equation
Secondary: 46E35: Sobolev spaces and other spaces of “smooth” functions, embedding theorems, trace theorems 42B37: Harmonic analysis and PDE
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 4 , August 2019 , pp. 983 - 995
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by Zhejiang Provincial Natural Science Foundation (No. LY16A010013) and National Natural Science Foundation of China (Grant No. 11471288). The work was done when the two authors were working together at Johns Hopkins University.

References

Besse, A., Manifolds all of whose geodesics are closed . Springer-Verlag, New York, 1978.Google Scholar
Bourgain, J., A remark on Schrödinger operators . Israel J. Math. 77(1992), 1–16. https://doi.org/10.1007/BF02808007.Google Scholar
Bourgain, J., Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations, I. Schrödinger equations . Geom. Funct. Anal. 3(1993), 107–156. https://doi.org/10.1007/BF01896020.Google Scholar
Bourgain, J., Moment inequalities for trigonometric polynomials with spectrum in curved hypersurfaces . Israel J. Math. 193(2013), 441–458. https://doi.org/10.1007/s11856-012-0077-1.Google Scholar
Bourgain, J., On the Schrödinger maximal function in higher dimension . J. Proc. Steklov Inst. Math. 280(2013), 46–60.Google Scholar
Burq, N., Gérard, P., and Tzvetkov, N., Strichartz inequalities and the nonlinear Schrödinger equation on compact manifolds . Amer. J. Math. 126(2004), 569–605. https://doi.org/10.1353/ajm.2004.0016.Google Scholar
Burq, N., Gérard, P., and Tzvetkov, N., On nonlinear Schrödinger equations in exterior domains . Ann. Inst. H. Poincaré-AN 21(2004), 295–318. https://doi.org/10.1016/j.anihpc.2003.03.002.Google Scholar
Carleson, L., Some analytic problems related to statistical mechanics, Euclidean harmonic analysis . Lecture Notes in Math. 779, Springer, Berlin, 1980, pp. 5–45.Google Scholar
Cowling, M., Pointwise behavior of solutions to Schrödinger equations, harmonic analysis . Lecture Notes in Math. 992, Springer, Berlin, 1983, pp. 83–90.Google Scholar
Doi, S., Smoothing effects of Schrödinger evolution groups on Riemannian manifolds . Duke Math. J. 82(1996), 679–706. https://doi.org/10.1215/S0012-7094-96-08228-9.Google Scholar
Doi, S., Smoothing effects for Schrödinger evolution equation and global behavior of geodesic flow . Math. Ann. 318(2000), 355–389. https://doi.org/10.1007/s002080000128.Google Scholar
Du, X., Guth, L., and Li, X., A sharp Schrodinger maximal estimate in ℝ2 . arxiv:1612.08946.Google Scholar
Dahlberg, B. E. J. and Kenig, C. E., A note on the almost everywhere behavior of solutions to the Schrödinger equation . Lecture Notes in Math. 908. Springer-Verlag, Berlin, 1982, pp. 205–208.Google Scholar
Hömander, L., The analysis of linear partial differential operators III: pseudo-differential operators . Springer-Verlag, Berlin, 2007.Google Scholar
Keel, M. and Tao, T., End point Strichartz estimates . Amer. J. of Math. 120(1998), 955–980. https://doi.org/10.1353/ajm.1998.0039.Google Scholar
Lee, S., On pointwise convergence of the solutions to Schrödinger equations in ℝ2 . Int. Math. Res. Not. (2006), Art. ID 32597, 1–21.Google Scholar
Lucá, R. and Rogers, K., An improved necessary condition for the Schrödinger maximal estimate. arxiv:1506.05325.Google Scholar
Moyua, A., Vargas, A., and Vega, L., Schrödinger maximal function and restriction properties of the Fourier transform . Int. Math. Res. Not. 16(1996), 793–815.Google Scholar
Moyua, A. and Vega, L., Bounds for the maximal function associated to periodic solutions of one-dimensional dispersive equations . Bull. Lond. Math. Soc. 40(2008), no. 1, 117–128. https://doi.org/10.1112/blms/bdm096.Google Scholar
Sjölin, P., Regularity of solutions to the Schrödinger equation . Duke Math. J. 55(1987), 699–715. https://doi.org/10.1215/S0012-7094-87-05535-9.Google Scholar
Sjölin, P., Fourier integrals in classical analysis . Cambridge Tracts in Mathematics, 105. Cambridge University Press, Cambridge, 1993.Google Scholar
Sjölin, P., Concerning the L p norm of spectral clusters for second-order elliptic operators on compact manifolds . J. Funct. Anal. 77(1988), 123–138. https://doi.org/10.1016/0022-1236(88)90081-X.Google Scholar
Tao, T. and Vargas, A., A bilinear approach to cone multipliers. I. Restriction estimates . Geom. Funct. Anal. 10(2000), 185–215. https://doi.org/10.1007/s000390050006.Google Scholar
Tao, T. and Vargas, A., A bilinear approach to cone multipliers. II. Applications . Geom. Funct. Anal. 10(2000), 216–258. https://doi.org/10.1007/s000390050007.Google Scholar
Vega, L., Schrödinger equations: pointwise convergence to the initial data . Proc. Amer. Math. Soc. 102(1988), 874–878.Google Scholar
Walther, B. G., Some L p (L 1)- and L 2(L 2)- estimates for oscillatory Fourier transforms . In: Analysis of Divergence, 213–231 , Appl. Numer. Harmon. Anal., Birkhäuser Boston, Boston, MA, 1999, pp. 213–231.Google Scholar