Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-16T04:42:30.562Z Has data issue: false hasContentIssue false
  • English
  • Français

Free Product C*-algebras Associated with Graphs, Free Differentials, and Laws of Loops

Published online by Cambridge University Press:  20 November 2018

Michael Hartglass
Michael Hartglass*
Affiliation:
Department of Mathematics, UC Riverside, Riverside 92521, USA e-mail: michael.hartglass@ucr.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a canonical 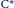${{\text{C}}^{*}}$-algebra, 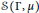$\text{S}\left( \Gamma ,\mu \right)$, that arises from a weighted graph 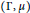$\left( \Gamma ,\mu \right)$, specific cases of which were previously studied in the context of planar algebras. We discuss necessary and sufficient conditions of the weighting that ensure simplicity and uniqueness of trace of 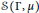$\text{S}\left( \Gamma ,\mu \right)$, and study the structure of its positive cone. We then study the $*$-algebra, 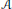$\mathcal{A}$, generated by the generators of 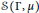$\text{S}\left( \Gamma ,\mu \right)$, and use a free differential calculus and techniques of Charlesworth and Shlyakhtenko as well as Mai, Speicher, and Weber to show that certain “loop” elements have no atoms in their spectral measure. After modifying techniques of Shlyakhtenko and Skoufranis to show that self adjoint elements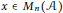$x\,\in \,{{M}_{n}}\left( \mathcal{A} \right)$ have algebraic Cauchy transform, we explore some applications to eigenvalues of polynomials in Wishart matrices and to diagrammatic elements in von Neumann algebras initially considered by Guionnet, Jones, and Shlyakhtenko.

Keywords

46L09free probabilityC* -algebra
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 69 , Issue 3 , 01 June 2017 , pp. 548 - 578
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Avi82] Avitzour, D., Free products of C*-algebras. Trans. Amer. Math. Soc. 271(1982), no. 2, 423–435.http://dx.doi.Org/10.2307/1998890 Google Scholar
[BG05] Benaych-Georges, F., Rectangular random matrices, related free entropy and free fisher's information. arxiv:math/051 2081 Google Scholar
[BHP12] Brothier, A., Hartglass, M., and Penneys, D., Rigid C*-tensor categories of bimodules over interpolated free group factors. J. Math. Phys. 53(2012), no. 12,123525.http://dx.doi.Org/10.1063/1.4769178 Google Scholar
[Bis97] Bisch, D., Bimodules, higher relative commutants and the fusion algebra associated to a subfactor. In: Operator algebras and their applications (Waterloo, ON, 1994/1995), Fields Inst. Commun., 13, Amer. Math. Soc, Providence, RI, 1997, pp. 13–63.Google Scholar
[CDS14] Curran, S., Dabrowski, Y., and Shlyakhtenko, D., Free analysis and planar algebras. arxiv:1411.0268 Google Scholar
[CK80] Cuntz, J. and Krieger, W., A class of C*-algebras and topological Markov chains. Invent. Math. 56(1980), no. 3, 251–268.http://dx.doi.org/10.1007/BF01390048 Google Scholar
[CS15] Charlesworth, I. and Shlyakhtenko, D., Regularity of polynomials in free variables. arxiv:1408.0580v2 Google Scholar
[Dyk93] Dykema, K., Free products of hyperfinite von Neumann algebras and free dimension. Duke Math. J. 69(1993), no. 1, 97–119. http://dx.doi.org/10.1090/S0002-9947-99-02180-7 Google Scholar
[Dyk99] Dykema, K. J., Simplicity and the stable rank of some free product C* -algebras. Trans. Amer. Math. Soc. 351(1999), no. 1, 1–40.http://dx.doi.org/10.1090/S0002-9947-99-02180-7 Google Scholar
[DHR97] Dykema, K., Haagerup, U., and Rordam, M., The stable rank of some free product C* -algebras. Duke Math. J. 90(1997), no. 1, 95–121.http://dx.doi.org/10.1215/s0012-7094-97-09004-9 Google Scholar
[DR13] Dykema, K. J. and Redelmeier, D., The amalgamated free product of hyperfinite von Neumann algebras over finite dimensional subalgebras. Houston J. Math. 39(2013), no. 4,1313–1331.Google Scholar
[DR98] Dykema, K.J. and Rørdam, M., Projections in free product C* -algebras. Geom. Funct. Anal. 8(1998), no. 1, 1–16.http://dx.doi.org/10.1007/s000390050046 Google Scholar
[Ger] Germain, E., KK-theory of C* -algebras related to Pimsner algebras. http://www.math.jussieu.fr/-germain Google Scholar
[GJS10] Guionnet, A., Jones, V. E R., and Shlyakhtenko, D. , Random matrices, free probability, planar algebras and subfactors. In: Quanta of maths, Clay Math. Proc, 11, Amer. Math. Soc, Providence, RI, 2010, pp. 201–239.Google Scholar
[GJS11] Guionnet, A., A semi-finite algebra associated to a subf actor planar algebra. J. Funct. Anal. 261(2011), no. 5, 1345–1360.http://dx.doi.Org/10.1016/j.jfa.2O11.05.004 Google Scholar
[Harl3] Hartglass, M., Free product von Neumann algebras associated to graphs, and Guionnet, Jones, Shlyakhtenko subfactors in infinite depth. J. Funct. Anal. 265(2013), no. 12, 3305–3324. http://dx.doi.Org/10.1016/j.jfa.2013.09.011 Google Scholar
[HP14a] Hartglass, M. and Penneys, D., C* -algebras from planar algebras I: canonical C* -algebras associated to a planar algebra. Trans. Amer. Math. Soc, to appear. arxiv:1401.2485 Google Scholar
[HP14b] Hartglass, M., C* -algebras from planar algebras II: The Guionnet--Jones-Shlyakhtenko C* -algebras. J. Funct. Anal. 267(2014), no. 10, 3859–3893.http://dx.doi.Org/10.1016/j.jfa.2O14.08.024 Google Scholar
[Ivall] Ivanov, N. A., On the structure of some reduced amalgamated free product C* -algebras. Internat. J. Math. 22(2011), no. 2, 281–306.http://dx.doi.Org/10.1142/S0129167X11006799 Google Scholar
[Jon83] Jones, V. F. R., Index for subfactors. Invent. Math. 72(1983), no. 1,1–25, http://dx.doi.Org/10.1007/BF01389127 Google Scholar
[MSW14] Mai, T., Speicher, R., Absence of algebraic relations and of zero divisors under the assumption of finite non-microstates free fisher information. arxiv:1407.5715 Google Scholar
[PetlO] Peters, E., A planar algebra construction of the Haagerup subfactor. Internat. J. Math. 21(2010), no. 8, 987–1045. http://dx.doi.Org/10.1142/S0129167X10006380 Google Scholar
[Pim97] Pimsner, M. V.,A class of C* -algebras generalizing both Cuntz-Krieger algebras and crossed products by Z. In: Free probability theory (Waterloo, ON, 1995), Fields Inst. Commun., 12, American Mathematical Society, Providence, RI, 1997, pp. 189–212.Google Scholar
[Pop95] Popa, S., An axiomatization of the lattice of higher relative commutants of a subfactor. Invent. Math. 120(1995), no. 3, 427–445,http://dx.doi.org/10.1007/BF01241137 Google Scholar
[Rie83] M. A.|Rieffel, Dimension and stable rank in the K-theory of C* -algebras. Proc. London Math. Soc. (3) 46(1983), no. 2, 301–333.http://dx.doi.Org/10.111 2/plms/s3-46.2.301 Google Scholar
[SauO3] Sauer, R., Power series over the group ring of a free group and applications to Novikov-Shubin invariants. In: High-dimensional manifold topology, World Sci. Publ., River Edge, NJ, 2003, pp. 449–468.http://dx.doi.Org/10.1142/9789812704443J3020 Google Scholar
[Sch62] Schiitzenberger, M. P., On a theorem of R.Jungen. Proc. Amer. Math. Soc. 13(1962), 885–890. http://dx.doi.Org/10.2307/2034080 Google Scholar
[Shl99] Shlyakhtenko, D.,A-valued semicircular systems. J. Funct. Anal. 166(1999), no. 1,1–47. http://dx.doi.org/10.1006/jfan.1999.3424 Google Scholar
[SS15] Shlyakhtenko, D. and Skoufranis, P., Freely independent random variables with non-atomic distributions. Trans. Amer. Math. Soc. 367(2015), no. 9, 6267–6291. http://dx.doi.org/10.1090/S0002-9947-2015-06434-4 Google Scholar
[VDN92] Voiculescu, D. V., Dykema, K. J., and Nica, A., Free random variables. CRM Monograph Series, 1, American Mathematical Society, Providence, RI, 1992.Google Scholar
[Voi93] Voiculescu, D. V., The analogues of entropy and of Fisher-s information measure in free probability theory. I. Comm. Math. Phys. 155(1993), no. 1, 71–92. http://dx.doi.org/10.1007/BF02100050 Google Scholar