 |
|
Global Well-Posedness and Convergence Results for 3D-Regularized Boussinesq System |
Published:2012-08-25
Printed: Dec 2012
Printed: Dec 2012
- Ridha Selmi,
Abstract
Analytical study to the regularization of the Boussinesq system is
performed in frequency space using Fourier theory. Existence and
uniqueness of weak solution with minimum regularity requirement are
proved. Convergence results of the unique weak solution of the
regularized Boussinesq system to a weak Leray-Hopf solution of the
Boussinesq system are established as the regularizing parameter
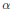$\alpha$ vanishes. The proofs are done in the frequency space and use
energy methods, Arselà-Ascoli compactness theorem and a Friedrichs
like approximation scheme.
| Keywords: | regularizing Boussinesq system, existence and uniqueness of weak solution, convergence results, compactness method in frequency space |
| MSC Classifications: |
35A05 - General existence and uniqueness theorems 76D03 - Existence, uniqueness, and regularity theory [See also 35Q30] 35B40 - Asymptotic behavior of solutions 35B10 - Periodic solutions 86A05 - Hydrology, hydrography, oceanography [See also 76Bxx, 76E20, 76Q05, 76Rxx, 76U05] 86A10 - Meteorology and atmospheric physics [See also 76Bxx, 76E20, 76N15, 76Q05, 76Rxx, 76U05] |
