No CrossRef data available.
Article contents
Optimal Polynomial Recurrence
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 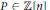 $P\in \mathbb{Z}\left[ n \right]$ with
$P\in \mathbb{Z}\left[ n \right]$ with 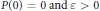 $P(0)\,=\,0\,\text{and}\,\varepsilon \,>\,0$. We show, using Fourier analytic techniques, that if
$P(0)\,=\,0\,\text{and}\,\varepsilon \,>\,0$. We show, using Fourier analytic techniques, that if 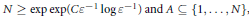 $N\ge \exp \exp \left( C{{\varepsilon }^{-1}}\log {{\varepsilon }^{-1}} \right)\,\text{and}\,A\,\subseteq \,\left\{ 1,\,.\,.\,.\,,\,N \right\}$ then there must exist
$N\ge \exp \exp \left( C{{\varepsilon }^{-1}}\log {{\varepsilon }^{-1}} \right)\,\text{and}\,A\,\subseteq \,\left\{ 1,\,.\,.\,.\,,\,N \right\}$ then there must exist 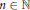 $n\in \mathbb{N}$ such that
$n\in \mathbb{N}$ such that
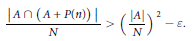 $$\frac{\left| A\cap \left( A+P\left( n \right) \right) \right|}{N}>{{\left( \frac{\left| A \right|}{N} \right)}^{2}}-\,\varepsilon $$
$$\frac{\left| A\cap \left( A+P\left( n \right) \right) \right|}{N}>{{\left( \frac{\left| A \right|}{N} \right)}^{2}}-\,\varepsilon $$
In addition to this we show, using the same Fourier analytic methods, that if 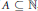 $A\subseteq \mathbb{N}$, then the set
of
$A\subseteq \mathbb{N}$, then the set
of  $\varepsilon $-optimal return times
$\varepsilon $-optimal return times
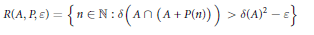 $$R\left( A,P,\varepsilon \right)=\left\{ n\in \mathbb{N}:\delta \left( A\cap \left. \left( A+P\left( n \right) \right) \right)> \right.\delta {{\left( A \right)}^{2}}-\varepsilon \right\}$$
$$R\left( A,P,\varepsilon \right)=\left\{ n\in \mathbb{N}:\delta \left( A\cap \left. \left( A+P\left( n \right) \right) \right)> \right.\delta {{\left( A \right)}^{2}}-\varepsilon \right\}$$
is syndetic for every 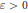 $\varepsilon >0$. Moreover, we show that
$\varepsilon >0$. Moreover, we show that 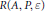 $R\left( A,\,P,\,\varepsilon \right)$ is dense in every sufficiently long interval, in particular we show that there exists an
$R\left( A,\,P,\,\varepsilon \right)$ is dense in every sufficiently long interval, in particular we show that there exists an 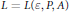 $L=L\left( \varepsilon ,P,A \right)$ such that
$L=L\left( \varepsilon ,P,A \right)$ such that
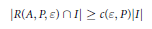 $$\left| R\left( A,P,\varepsilon \right)\cap I \right|\ge c\left( \varepsilon ,P \right)\left| I \right|$$
$$\left| R\left( A,P,\varepsilon \right)\cap I \right|\ge c\left( \varepsilon ,P \right)\left| I \right|$$
for all intervals 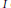 $I$ of natural numbers with
$I$ of natural numbers with 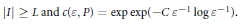 $\left| I \right|\,\ge \,L\,\text{and}\,c\left( \varepsilon ,\,P \right)\,=\,\exp \exp \,\left( -C\,{{\varepsilon }^{-1}}\,\log {{\varepsilon }^{-1}} \right).$
$\left| I \right|\,\ge \,L\,\text{and}\,c\left( \varepsilon ,\,P \right)\,=\,\exp \exp \,\left( -C\,{{\varepsilon }^{-1}}\,\log {{\varepsilon }^{-1}} \right).$
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013




