Rectifiability of Optimal Transportation Plans

http://dx.doi.org/10.4153/CJM-2011-080-6
Canad. J. Math. 64(2012), 924-933

  Published:2011-11-03
 Printed: Aug 2012

The regularity of solutions to optimal transportation problems has become a hot topic in current research. It is well known by now that the optimal measure may not be concentrated on the graph of a continuous mapping unless both the transportation cost and the masses transported satisfy very restrictive hypotheses (including sign conditions on the mixed fourth-order derivatives of the cost function). 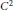The purpose of this note is to show that in spite of this, the optimal measure is supported on a Lipschitz manifold, provided only that the cost is $C^{2}$ with non-singular mixed second derivative. We use this result to provide a simple proof that solutions to Monge's optimal transportation problem satisfy a change of variables equation almost everywhere.