Article contents
BMO-Estimates for Maximal Operators via Approximations of the Identity with Non-Doubling Measures
Published online by Cambridge University Press: 20 November 2018
Abstract
Let  $\mu $ be a nonnegative Radon measure on
$\mu $ be a nonnegative Radon measure on 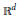 ${{\mathbb{R}}^{d}}$ that satisfies the growth condition that there exist constants
${{\mathbb{R}}^{d}}$ that satisfies the growth condition that there exist constants 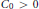 ${{C}_{0}}\,>\,0$ and
${{C}_{0}}\,>\,0$ and 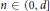 $n\,\in \,(0,\,d]$ such that for all
$n\,\in \,(0,\,d]$ such that for all 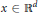 $x\,\in \,{{\mathbb{R}}^{d}}$ and
$x\,\in \,{{\mathbb{R}}^{d}}$ and 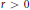 $r\,>\,0$,
$r\,>\,0$, 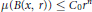 $\mu \left( B\left( x,\,r \right) \right)\,\le \,{{C}_{0}}{{r}^{n}}$, where
$\mu \left( B\left( x,\,r \right) \right)\,\le \,{{C}_{0}}{{r}^{n}}$, where 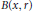 $B(x,\,r)$ is the open ball centered at
$B(x,\,r)$ is the open ball centered at  $x$ and having radius
$x$ and having radius  $r$. In this paper, the authors prove that if
$r$. In this paper, the authors prove that if 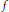 $f$ belongs to the
$f$ belongs to the 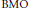 $\text{BMO}$-type space
$\text{BMO}$-type space 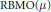 $\text{RBMO(}\mu \text{)}$ of Tolsa, then the homogeneous maximal function
$\text{RBMO(}\mu \text{)}$ of Tolsa, then the homogeneous maximal function 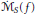 ${{\dot{\mathcal{M}}}_{s}}\left( f \right)$ (when
${{\dot{\mathcal{M}}}_{s}}\left( f \right)$ (when
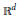 ${{\mathbb{R}}^{d}}$ is not an initial cube) and the inhomogeneous maximal function
${{\mathbb{R}}^{d}}$ is not an initial cube) and the inhomogeneous maximal function 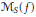 ${{\overset{{}}{\mathop{\mathcal{M}}}\,}_{s}}\left( f \right)$ (when
${{\overset{{}}{\mathop{\mathcal{M}}}\,}_{s}}\left( f \right)$ (when 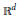 ${{\mathbb{R}}^{d}}$ is an initial cube) associated with a given approximation of the identity
${{\mathbb{R}}^{d}}$ is an initial cube) associated with a given approximation of the identity  $S $ of Tolsa are either infinite everywhere or finite almost everywhere, and in the latter case,
$S $ of Tolsa are either infinite everywhere or finite almost everywhere, and in the latter case, 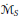 ${{\dot{\mathcal{M}}}_{s}}$ and
${{\dot{\mathcal{M}}}_{s}}$ and 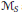 ${{\mathcal{M}}_{s}}$ are bounded from
${{\mathcal{M}}_{s}}$ are bounded from 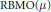 $\text{RBMO(}\mu \text{)}$ to the
$\text{RBMO(}\mu \text{)}$ to the 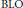 $\text{BLO}$-type space
$\text{BLO}$-type space 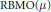 $\text{RBMO(}\mu \text{)}$. The authors also prove that the inhomogeneous maximal operator
$\text{RBMO(}\mu \text{)}$. The authors also prove that the inhomogeneous maximal operator 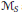 ${{\mathcal{M}}_{s}}$ is bounded from the local
${{\mathcal{M}}_{s}}$ is bounded from the local 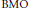 $\text{BMO}$-type space
$\text{BMO}$-type space 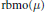 $\text{rbmo(}\mu \text{)}$ to the local
$\text{rbmo(}\mu \text{)}$ to the local 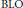 $\text{BLO}$-type space
$\text{BLO}$-type space 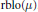 $\text{rblo(}\mu \text{)}$.
$\text{rblo(}\mu \text{)}$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
Footnotes
Dachun Yang is supported by National Science Foundation for Distinguished Young Scholars (No. 10425106) and NCET (No. 04-0142) of Ministry of Education of China.
References
- 2
- Cited by




