Hostname: page-component-8448b6f56d-m8qmq Total loading time: 0 Render date: 2024-04-24T13:45:16.954Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Order Scattering on Asymptotically Euclidean Manifolds

Published online by Cambridge University Press:  20 November 2018

T. J. Christiansen  and
M. S. Joshi
T. J. Christiansen
Affiliation:
Department of Mathematics, University of Missouri, Columbia, Missouri 65211, USA email: tjc@math.missouri.edu
M. S. Joshi
Affiliation:
Darwin College, Cambridge CB3 9EU, UK
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop a scattering theory for perturbations of powers of the Laplacian on asymptotically Euclidean manifolds. The (absolute) scattering matrix is shown to be a Fourier integral operator associated to the geodesic flow at time $\pi $ on the boundary. Furthermore, it is shown that on 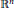${{\mathbb{R}}^{n}}$ the asymptotics of certain short-range perturbations of 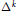${{\Delta }^{k}}$ can be recovered from the scattering matrix at a finite number of energies.

Keywords

58G15scattering theoryconormalLagrangian
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 52 , Issue 5 , 01 October 2000 , pp. 897 - 919
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Agmon, S., Spectral Properties of Schrödinger Operators and Scattering Theory. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 2(1975), 151–218.Google Scholar
[2] Agmon, S. and Hörmander, L., Asymptotic Properties of Solutions of Differential Equations with Simple Characteristics. J. Analyse Math. 30(1976), 1–38.Google Scholar
[3] Bailey, T. B. and Eastwood, M. E., Zero-energy Fields on Real Projective Space. Geom. Dedicata 67(1997), 245–258.Google Scholar
[4] Christiansen, T., Weyl Asymptotics for the Laplacian on Asymptotically Euclidean Spaces. Amer. J. Math. 121(1999), 1–22.Google Scholar
[5] Hassell, A. and Vasy, A., The spectral projections and the resolvent for scattering metrics. J. Anal. Math., to appear.Google Scholar
[6] Helgasson, S., Groups and Geometric Analysis. Academic Press, New York, 1984.Google Scholar
[7] Hörmander, L., The Analysis of Linear Partial Differential Operators. Springer-Verlag, Berlin-Heidelberg-New York-Tokyo, 1983.Google Scholar
[8] Joshi, M. S., Recovering Asymptotics of Coulomb-like Potentials from Fixed Energy Scattering Data. SIAM J. Math. Anal. 30(1999), 516–526.Google Scholar
[9] Joshi, M. S., Explicitly Recovering Asymptotics of Short Range Potentials. Comm. Partial Differential Equations, to appear.Google Scholar
[10] Joshi, M. S. and Sá Barreto, A., Recovering Asymptotics of Short Range Potentials. Comm. Math. Phys. 193(1998), 197–208.Google Scholar
[11] Joshi, M. S. and Sá Barreto, A., Recovering Asymptotics ofMetrics fromFixed Energy Scattering Data. Invent.Math. 137(1999), 127–143.Google Scholar
[12] Joshi, M. S. and Sá Barreto, A., Determining Asymptotics of Magnetic Potentials from Fixed Energy Scattering Data. Asymptotic Anal. 21(1999), 61–70.Google Scholar
[13] Liu, C., A Uniqueness Result for a General Class of Inverse Problems. Comm. Partial Differential Equations 21(1996), 1951–1983.Google Scholar
[14] Melrose, R. B., Spectral and Scattering Theory for the Laplacian on Asymptotically Euclidean spaces. Ed. M. Ikawa, Marcel Dekker, New York, 1994.Google Scholar
[15] Melrose, R. B. and Zworski, M., Scattering Metrics and Geodesic Flow at Infinity. Invent. Math. 124(1996), 389–436.Google Scholar
[16] Parnovski, L., Scattering Matrix for Manifolds with Conical Ends. Preprint.Google Scholar
[17] Reed, M. and Simon, B., Methods of Modern Mathematical Physics: Vol III, Scattering Theory. Academic Press, New York, 1979.Google Scholar
[18] Vasy, A., Geometric Scattering Theory for Long-Range Potentials and Metrics. Internat.Math. Res. Notices (6) 1998, 285–315.Google Scholar