Article contents
Asymptotic Shape of Finite Packings
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 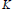 $K$ be a convex body in
$K$ be a convex body in
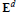 ${{\mathbf{E}}^{d}}$ and denote by
${{\mathbf{E}}^{d}}$ and denote by
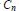 ${{C}_{n}}$ the set of centroids of
${{C}_{n}}$ the set of centroids of  $n$ non-overlapping translates of
$n$ non-overlapping translates of 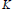 $K$. For
$K$. For 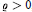 $\varrho \,>\,0$, assume that the parallel body conv
$\varrho \,>\,0$, assume that the parallel body conv
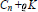 ${{C}_{n}}\,+\,\varrho K$ of conv
${{C}_{n}}\,+\,\varrho K$ of conv 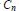 ${{C}_{n}}$ has minimal volume. The notion of parametric density (see [21]) provides a bridge between finite and infinite packings (see [4] or [14]). It is known that there exists a maximal
${{C}_{n}}$ has minimal volume. The notion of parametric density (see [21]) provides a bridge between finite and infinite packings (see [4] or [14]). It is known that there exists a maximal 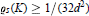 ${{\varrho }_{s}}(K)\,\ge \,1/(32{{d}^{2}})$ such that conv
${{\varrho }_{s}}(K)\,\ge \,1/(32{{d}^{2}})$ such that conv 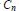 ${{C}_{n}}$ is a segment for
${{C}_{n}}$ is a segment for 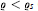 $\varrho \,<\,{{\varrho }_{s}}$ (see [5]). We prove the existence of a minimal
$\varrho \,<\,{{\varrho }_{s}}$ (see [5]). We prove the existence of a minimal 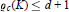 ${{\varrho }_{c}}(K)\,\le \,d\,+\,1$ such that if
${{\varrho }_{c}}(K)\,\le \,d\,+\,1$ such that if 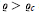 $\varrho \,>\,{{\varrho }_{c}}$ and
$\varrho \,>\,{{\varrho }_{c}}$ and  $n$ is large then the shape of conv
$n$ is large then the shape of conv 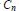 ${{C}_{n}}$ can not be too far from the shape of
${{C}_{n}}$ can not be too far from the shape of 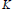 $K$. For
$K$. For 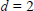 $d\,=\,2$, we verify that
$d\,=\,2$, we verify that 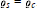 ${{\varrho }_{s\,}}\,=\,{{\varrho }_{c}}$. For
${{\varrho }_{s\,}}\,=\,{{\varrho }_{c}}$. For 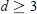 $d\,\ge \,3$, we present the first example of a convex body with known
$d\,\ge \,3$, we present the first example of a convex body with known 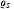 ${{\varrho }_{s}}$ and
${{\varrho }_{s}}$ and 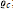 ${{\varrho }_{c}}$; namely, we have
${{\varrho }_{c}}$; namely, we have 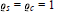 ${{\varrho }_{s}}\,=\,{{\varrho }_{c}}\,=\,1$ for the parallelotope.
${{\varrho }_{s}}\,=\,{{\varrho }_{c}}\,=\,1$ for the parallelotope.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1998
References
- 2
- Cited by




