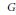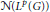Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Neufang, Matthias
and
Runde, Volker
2007.
Harmonic operators: the dual perspective.
Mathematische Zeitschrift,
Vol. 255,
Issue. 3,
p.
669.
Jaworski, Wojciech
and
Neufang, Matthias
2007.
The Choquet–Deny Equation in a Banach Space.
Canadian Journal of Mathematics,
Vol. 59,
Issue. 4,
p.
795.
Kalantar, Mehrdad
and
Neufang, Matthias
2013.
Duality, cohomology, and geometry of locally compact quantum groups.
Journal of Mathematical Analysis and Applications,
Vol. 406,
Issue. 1,
p.
22.
Crann, Jason
and
Neufang, Matthias
2015.
Amenability and covariant injectivity of locally compact quantum groups.
Transactions of the American Mathematical Society,
Vol. 368,
Issue. 1,
p.
495.
Soltani Renani, S.
and
Yari, Z.
2023.
Projectivity of Some Banach Right Modules over the Group Algebra ℓ1(G).
Analysis Mathematica,
Vol. 49,
Issue. 3,
p.
881.
Soltani Renani, S.
and
Yari, Z.
2024.
Character Contractibility and Amenability of Banach Algebras with Applications to Quantum Groups.
Siberian Mathematical Journal,
Vol. 65,
Issue. 2,
p.
448.