http://dx.doi.org/10.4153/CJM-2012-031-3
16 pages
Published:2012-09-08
Peter J. Cho, Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4 Henry H. Kim, Department of Mathematics, University of Toronto, Toronto, ON M5S 2E4
Features coming soon:
Citations (via CrossRef)
Tools:
Search Google Scholar:
Abstract
We construct unconditionally several families of number fields with
the largest possible class numbers. They are number fields of degree 4
and 5 whose Galois closures have the Galois group 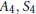$A_4, S_4$ and
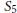$S_5$. We first construct families of number fields with smallest
regulators, and by using the strong Artin conjecture and applying zero
density result of Kowalski-Michel, we choose subfamilies of
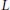$L$-functions which are zero free close to 1.
For these subfamilies, the 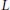$L$-functions have the extremal value at
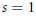$s=1$, and by the class number formula, we obtain the extreme class
numbers.
| MSC Classifications: |
11R29, 11M41 show english descriptions
Class numbers, class groups, discriminants
Other Dirichlet series and zeta functions {For local and global ground fields, see 11R42, 11R52, 11S40, 11S45; for algebro-geometric methods, see 14G10; see also 11E45, 11F66, 11F70, 11F72}
11R29 - Class numbers, class groups, discriminants
11M41 - Other Dirichlet series and zeta functions {For local and global ground fields, see 11R42, 11R52, 11S40, 11S45; for algebro-geometric methods, see 14G10; see also 11E45, 11F66, 11F70, 11F72}
|
© Canadian Mathematical Society, 2013
| 
