Article contents
A Fractal Function Related to the John–Nirenberg Inequality for Qα(ℝn)
Published online by Cambridge University Press: 20 November 2018
Abstract
A borderline case function 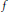 $f$ for
$f$ for 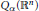 ${{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$ spaces is defined as a Haar wavelet decomposition, with the coefficients depending on a fixed parameter
${{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$ spaces is defined as a Haar wavelet decomposition, with the coefficients depending on a fixed parameter 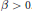 $\beta \,>\,0$. On its support
$\beta \,>\,0$. On its support 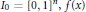 ${{I}_{0}}\,=\,{{\left[ 0,\,1 \right]}^{n}},\,f\left( x \right)$ can be expressed by the binary expansions of the coordinates of
${{I}_{0}}\,=\,{{\left[ 0,\,1 \right]}^{n}},\,f\left( x \right)$ can be expressed by the binary expansions of the coordinates of  $x$. In particular,
$x$. In particular, 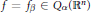 $f\,=\,{{f}_{\beta }}\,\in \,{{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$ if and only if
$f\,=\,{{f}_{\beta }}\,\in \,{{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$ if and only if 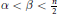 $\alpha \,<\,\beta \,<\frac{n}{2}$
, while for
$\alpha \,<\,\beta \,<\frac{n}{2}$
, while for 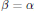 $\beta \,=\,\alpha $, it was shown by Yue and Dafni that
$\beta \,=\,\alpha $, it was shown by Yue and Dafni that 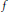 $f$ satisfies a John–Nirenberg inequality for
$f$ satisfies a John–Nirenberg inequality for 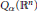 ${{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$. When
${{Q}_{\alpha }}\left( {{\mathbb{R}}^{n}} \right)$. When 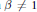 $\beta \,\ne \,1$,
$\beta \,\ne \,1$, 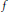 $f$ is a self-affine function. It is continuous almost everywhere and discontinuous at all dyadic points inside
$f$ is a self-affine function. It is continuous almost everywhere and discontinuous at all dyadic points inside 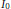 ${{I}_{0}}$. In addition, it is not monotone along any coordinate direction in any small cube. When the parameter
${{I}_{0}}$. In addition, it is not monotone along any coordinate direction in any small cube. When the parameter 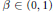 $\beta \,\in \,\left( 0,\,1 \right)$,
$\beta \,\in \,\left( 0,\,1 \right)$, 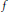 $f$ is onto from
$f$ is onto from 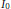 ${{I}_{0}}$ to
${{I}_{0}}$ to
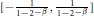 $\left[ -\frac{1}{1-{{2}^{-\beta }}},\,\frac{1}{1-{{2}^{-\beta }}} \right]$
, and the graph of
$\left[ -\frac{1}{1-{{2}^{-\beta }}},\,\frac{1}{1-{{2}^{-\beta }}} \right]$
, and the graph of 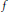 $f$ has a non-integer fractal dimension
$f$ has a non-integer fractal dimension 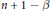 $n\,+\,1\,-\beta$.
$n\,+\,1\,-\beta$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2010
Footnotes
Supported in part by NSERC and the CRM, Montréal.
References
- 1
- Cited by




