Article contents
Convex Subordination Chains in Several Complex Variables
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this paper we study the notion of a convex subordination chain in several complex variables. We obtain certain necessary and sufficient conditions for a mapping to be a convex subordination chain, and we give various examples of convex subordination chains on the Euclidean unit ball in 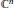 ${{\mathbb{C}}^{n}}$. We also obtain a sufficient condition for injectivity of
${{\mathbb{C}}^{n}}$. We also obtain a sufficient condition for injectivity of 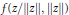 $f(z/\|z\|,\,\,\|z\|)$ on
$f(z/\|z\|,\,\,\|z\|)$ on 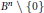 ${{B}^{n}}\backslash \{0\}$, where
${{B}^{n}}\backslash \{0\}$, where 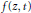 $f(z,t)$ is a convex subordination chain over
$f(z,t)$ is a convex subordination chain over 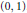 $(0,1)$.
$(0,1)$.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2009
References
[1]
Evans, L. C., Partial differential equations.
Graduate Studies in Mathematics 19, American Mathematical Society, Providence, RI, 1998.Google Scholar
[2]
Gong, S., Convex and starlike mappings in several complex variables.
Mathematics and its Applications 435, Kluwer Academic Publishers, Dordrecht, 1998.Google Scholar
[3]
Gong, S., Liu, T., On the Roper-Suffridge extension operator.
J. Anal. Math. 88(2002), 397–404.Google Scholar
[4]
Graham, I., Hamada, H., and Kohr, G., Parametric representation of univalent mappings in several complex variables.
Canad. J. Math. 54(2002), no. 2, 324–351.Google Scholar
[5]
Graham, I., Hamada, H., and Kohr, G., Radius problems for holomorphic mappings on the unit ball in
Cn. Math. Nachr. 279(2006), no. 13-14, 1474–1490.Google Scholar
[6]
Graham, I. and Kohr, G., Univalent mappings associated with the Roper-Suffridge extension operator.
J. Anal. Math. 81(2000), 331–342.Google Scholar
[7]
Graham, I. and Kohr, G., Geometric function theory in one and higher dimensions.
Monographs and Textbooks in Pure and Applied Mathematics 255, Marcel Dekker Inc., New York, 2003.Google Scholar
[8]
Graham, I., Kohr, G., and Kohr, M., Loewner chains and the Roper-Suffridge extension operator.
J. Math. Anal. Appl. 247(2000), no. 2, 448–465.Google Scholar
[9]
Hamada, H. and Kohr, G., Simple criterions for strongly starlikeness and starlikeness of certain order. Math. Nachr. 254/255(2003), 165–171.Google Scholar
[10]
Hamada, H. and Kohr, G., Quasiconformal extension of biholomorphic mappings in several complex variables.
J. Anal. Math. 96(2005), 269–282.Google Scholar
[11]
Kohr, G., Kernel convergence and biholomorphic mappings in several complex variables.
Int. J. Math. Math. Sci. 67(2003), 4229–4239.Google Scholar
[12]
Kohr, G., Loewner chains and a modification of the Roper-Suffridge extension operator. Mathematica 48(71)(2006), no. 1, 41–48.Google Scholar
[13]
Megginson, R. E., An introduction to Banach space theory.
Graduate Texts in Mathematics 183, Springer-Verlag, New York, 1998.Google Scholar
[14]
Muir, J. R., Jr., A modification of the Roper-Suffridge extension operator.
Comput. Methods Funct. Theor. 5(2005), no. 1, 237–251.Google Scholar
[15]
Muir, J. R., A class of Loewner chain preserving extension operators.
J. Math. Anal. Appl. 337(2008, 862–879.Google Scholar
[16]
Muir, J. R., Jr. and Suffridge, T. J., Construction of convex mappings of p-balls in
C2. Comput. Methods Funct. Theor. 4(2004), no. 1, 21–34.Google Scholar
[17]
Muir, J. R., Jr. and Suffridge, T. J., A generalization of half-plane mappings to the ball in
Cn. Trans. Amer. Math. Soc. 359(2007), no. 4, 1485–1498.Google Scholar
[18]
Muir, J. R., Jr. and Suffridge, T. J., Extreme points for convex mappings of Bn.
J. Anal. Math. 98(2006), 169–182.Google Scholar
[19]
Pfaltzgraff, J. A., Subordination chains and univalence of holomorphic mappings in
Cn. Math. Ann. 210(1974), 55–68.Google Scholar
[20]
Pommerenke, C., Univalent functions.
Studia Mathematica/ Mathematische Lehrbücher 25, Vandenhoeck & Ruprecht, Göttingen, 1975.Google Scholar
[21]
Poreda, T., On the univalent holomorphic maps of the unit polydisc in
Cn which have the parametric representation. I. The geometrical properties. Ann. Univ. Mariae Curie-Sklodowska Sect. A. 41(1987), 105–113.Google Scholar
[22]
Poreda, T., On the univalent subordination chains of holomorphic mappings in Banach spaces.
Comment. Math. Prace Mat. 28(1989), no. 2, 295–304.Google Scholar
[23]
Roper, K. and Suffridge, T. J., Convex mappings on the unit ball of
Cn. J. Anal. Math. 65(1995), 333–347.Google Scholar
[24]
Roper, K. and Suffridge, T. J., Convexity properties of holomorphic mappings in
Cn. Trans. Amer. Math. Soc. 351(1999), no. 5, 1803–1833.Google Scholar
[25]
Ruscheweyh, S., Convolutions in geometric function theory.
Sèminaire de Mathèmatiques Supèrieures 83, Presses de l’Universit è de Montrèal, Montreal, Que., 1982.Google Scholar
[26]
Suffridge, T. J., The principle of subordination applied to functions of several variables.
Pacific J. Math. 33(1970), 241–248.Google Scholar
[27]
Suffridge, T. J., Starlikeness, convexity and other geometric properties of holomorphic maps in higher dimensions. In: Complex analysis, Lecture Notes in Math. 599, Springer-Verlag, Berlin, 1977, pp. 146–159.Google Scholar
- 2
- Cited by




