Hostname: page-component-76fb5796d-dfsvx Total loading time: 0 Render date: 2024-04-25T18:49:18.148Z Has data issue: false hasContentIssue false
  • English
  • Français

Algèbres de Lie d'homotopie associées à une proto-bigèbre de Lie

Published online by Cambridge University Press:  20 November 2018

Momo Bangoura
Momo Bangoura*
Affiliation:
Département de Mathématiques, Université de Conakry, BP 1147, République de Guinée email: angoura@gn.refer.org
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

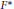On associe à toute structure de proto-bigèbre de Lie sur un espace vectoriel $F$ de dimension finie des structures d’algèbre de Lie d’homotopie définies respectivement sur la suspension de l’algèbre extérieure de $F$ et celle de son dual ${{F}^{*}}$. Dans ces algèbres, tous les crochets $n$-aires sont nuls pour 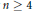$n\,\ge \,4$ du fait qu’ils proviennent d’une structure de proto-bigèbre de Lie. Plus généralement, on associe à un élément de degré impair de l’algèbre extérieure de la somme directe de $F$ et 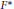${{F}^{*}}$, une collection d’applications multilinéaires antisymétriques sur l’algèbre extérieure de $F$ (resp. 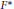${{F}^{*}}$), qui vérifient les identités de Jacobi généralisées, définissant les algèbres de Lie d’homotopie, si l’élément donné est de carré nul pour le grand crochet de l’algèbre extérieure de la somme directe de $F$ et de 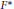${{F}^{*}}$.

Abstract

Abstract

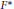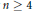To any proto-Lie algebra structure on a finite-dimensional vector space $F$, we associate homotopy Lie algebra structures defined on the suspension of the exterior algebra of $F$ and that of its dual ${{F}^{*}}$, respectively. In these algebras, all $n$-ary brackets for $n\,\ge \,4$ vanish because the brackets are defined by the proto-Lie algebra structure. More generally, to any element of odd degree in the exterior algebra of the direct sum of $F$ and 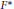${{F}^{*}}$, we associate a set of multilinear skew-symmetric mappings on the suspension of the exterior algebra of $F$ (resp. 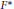${{F}^{*}}$), which satisfy the generalized Jacobi identities, defining the homotopy Lie algebras, if the given element is of square zero with respect to the big bracket of the exterior algebra of the direct sum of $F$ and 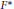${{F}^{*}}$.

Keywords

17B7017A30algèbre de Lie d'homotopiebigèbre de Liequasi-bigèbre de Lieproto-bigèbre de Liecrochet dérivéjacobiateur
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 4 , 01 August 2007 , pp. 696 - 711
Copyright
Copyright © Canadian Mathematical Society 2007

References

Références

[1] Akman, F. et Ionescu, L. M., Higher derived brackets and deformation theory I. arXiv:math.QA/0504541.Google Scholar
[2] Bangoura, M., Algèbres quasi-Gerstenhaber différentielles. Travaux mathématiques 16(2005), 299–314.Google Scholar
[3] De Wilde, M. et Lecomte, P., Formal deformations of the Poisson Lie algebra of a symplectic manifold and star-products. Existence, equivalence, derivations. Nato Adv. Sci. Inst. Ser. C Math. Phys. Sci. 247(1988), 897–960.Google Scholar
[4] Drinfeld, V. G., Hamiltonian structures on Lie groups, Lie bialgebras and the geometric meaning of classical Yang–Baxter equations. (Russian) Dokl. Akad. Nauk SSSR 268(1983), 285–287.Google Scholar
[5] Drinfeld, V. G., On almost cocommutative Hopf algebras. Leningrad Math. J. 1(1990), 331–342.Google Scholar
[6] Drinfeld, V. G., Quasi-Hopf algebras. Leningrad Math. J. 1(1990), 1419–1457.Google Scholar
[7] Huebschmann, J., Higher homotopies and Maurer–Cartan algebras: quasi-Lie Rinehart, Gerstenhaber, and Batalin–Vilkovisky algebras. Dans : The breadth of symplectic and Poisson geometry, Progr. Math. 232, Birkhäuser, Boston, 2005, 237–302.Google Scholar
[8] Kosmann-Schwarzbach, Y., Grand crochet, crochets de Schouten et cohomologie d’algèbres de Lie. C. R. Acad. Sci. Paris Sér. I Math. 312(1991), 123–126.Google Scholar
[9] Kosmann-Schwarzbach, Y., Jacobian quasi-bialgebras and quasi-Poisson Lie groups. Contemp. Math. 132(1992), 459–489.Google Scholar
[10] Kosmann-Schwarzbach, Y., From Poisson algebras to Gerstenhaber algebras. Ann. Inst. Fourier Grenoble 46(1996), 1243–1274.Google Scholar
[11] Kosmann-Schwarzbach, Y., Derived brackets. Lett. Math. Phys. 69(2004), 61–87.Google Scholar
[12] Kosmann-Schwarzbach, Y., Quasi, twisted, and all that… in Poisson geometry and Lie algebroid theory. Dans :The breadth of symplectic and Poisson geometry, Progr. Math. 232, Birkhäuser, Boston, 2005, 363–389.Google Scholar
[13] Kosmann-Schwarzbach, Y. et Magri, F., Poisson–Nijenhuis structures. Ann. Inst. Henri Poincaré A 53(1990), 35–81.Google Scholar
[14] Kostant, B. et Sternberg, S., Symplectic reduction, BRS cohomology, and infinite-dimensional Clifford algebras. Ann. Physics 176(1987), 49–113.Google Scholar
[15] Koszul, J.-L., Crochet de Schouten–Nijenhuis et cohomologie. Astérisque 1985(numéro hors série), Soc. Math. France, 257–271.Google Scholar
[16] Lada, T. et Markl, M., Strongly homotopy Lie algebras. Comm. Algebra 23(1995), 2147–2161.Google Scholar
[17] Lada, T. et Stasheff, J., Introduction to SH Lie algebras for physicists. Internat. J. Theoret. Physics 32(1993), 1087–1103.Google Scholar
[18] Lecomte, P. et Roger, C., Modules et cohomologie des bigèbres de Lie. C. R. Acad. Sci. Paris Sér. I 310(1990), 405–410.Google Scholar
[19] Roytenberg, D., Courant algebroids, derived brackets and even symplectic supermanifolds. Ph.D. thesis, Berkeley, 1999, mathDG/9910078.Google Scholar
[20] Roytenberg, D., Quasi-Lie bialgebroids and twisted Poisson manifolds. Lett. Math. Physics 61(2002), 123–137.Google Scholar
[21] Voronov, T., Higher derived brackets and homotopy algebras. J. Pure Appl. Algebra 202(2005), 133–153.Google Scholar
[22] Voronov, T., Higher derived brackets for arbitrary derivations. Travaux mathématiques 16(2005), 163–186.Google Scholar