Article contents
Computations of Elliptic Units for Real Quadratic Fields
Published online by Cambridge University Press: 20 November 2018
Abstract
Let 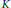 $K$ be a real quadratic field, and
$K$ be a real quadratic field, and 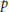 $p$ a rational prime which is inert in
$p$ a rational prime which is inert in 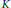 $K$. Let
$K$. Let 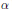 $\alpha $ be a modular unit on
$\alpha $ be a modular unit on 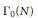 ${{\Gamma }_{0}}(N)$. In an earlier joint article with Henri Darmon, we presented the definition of an element
${{\Gamma }_{0}}(N)$. In an earlier joint article with Henri Darmon, we presented the definition of an element 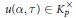 $u\left( \alpha ,\,\text{ }\!\!\tau\!\!\text{ } \right)\,\in \,K_{P}^{\times }$ attached to
$u\left( \alpha ,\,\text{ }\!\!\tau\!\!\text{ } \right)\,\in \,K_{P}^{\times }$ attached to 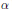 $\alpha $ and each
$\alpha $ and each 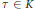 $\tau \,\in \,K$. We conjectured that the
$\tau \,\in \,K$. We conjectured that the 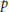 $p$-adic number
$p$-adic number 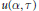 $u(\alpha ,\,\tau )$ lies in a specific ring class extension of
$u(\alpha ,\,\tau )$ lies in a specific ring class extension of 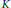 $K$ depending on
$K$ depending on 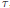 $\tau $, and proposed a “Shimura reciprocity law” describing the permutation action of Galois on the set of
$\tau $, and proposed a “Shimura reciprocity law” describing the permutation action of Galois on the set of 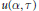 $u(\alpha ,\,\tau )$. This article provides computational evidence for these conjectures. We present an efficient algorithm for computing
$u(\alpha ,\,\tau )$. This article provides computational evidence for these conjectures. We present an efficient algorithm for computing 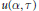 $u(\alpha ,\,\tau )$, and implement this algorithm with the modular unit
$u(\alpha ,\,\tau )$, and implement this algorithm with the modular unit 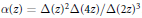 $\alpha (z)\,=\,\Delta {{(z)}^{2}}\,\Delta (4z)\,/\,\Delta {{(2z)}^{3}}$. Using
$\alpha (z)\,=\,\Delta {{(z)}^{2}}\,\Delta (4z)\,/\,\Delta {{(2z)}^{3}}$. Using 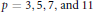 $p\,=\,3,\,5,\,7\,and\,11$, and all real quadratic fields
$p\,=\,3,\,5,\,7\,and\,11$, and all real quadratic fields 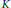 $K$ with discriminant
$K$ with discriminant 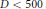 $D\,<\,500$ such that 2 splits in
$D\,<\,500$ such that 2 splits in 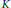 $K$ and
$K$ and 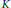 $K$ contains no unit of negative norm, we obtain results supporting our conjectures. One of the theoretical results in this paper is that a certain measure used to define
$K$ contains no unit of negative norm, we obtain results supporting our conjectures. One of the theoretical results in this paper is that a certain measure used to define 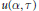 $u(\alpha ,\,\tau )$ is shown to be
$u(\alpha ,\,\tau )$ is shown to be 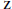 $\mathbf{Z}$-valued rather than only
$\mathbf{Z}$-valued rather than only 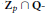 ${{\mathbf{Z}}_{P}}\,\cap \,\mathbf{Q}-$valued; this is an improvement over our previous result and allows for a precise definition of
${{\mathbf{Z}}_{P}}\,\cap \,\mathbf{Q}-$valued; this is an improvement over our previous result and allows for a precise definition of 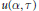 $u(\alpha ,\,\tau )$, instead of only up to a root of unity.
$u(\alpha ,\,\tau )$, instead of only up to a root of unity.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 8
- Cited by




