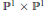We study the Hilbert functions of fat points in ${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. If 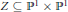$Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is an arbitrary fat point scheme, then it can be shown that for every 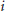$i$ and 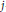$j$ the values of the Hilbert function 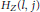${{H}_{Z}}(l,\,j)$ and 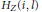${{H}_{Z}}(i,\,l)$ eventually become constant for 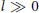$l\,\gg \,0$. We show how to determine these eventual values by using only the multiplicities of the points, and the relative positions of the points in 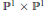${{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$. This enables us to compute all but a finite number values of 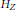${{H}_{Z}}$ without using the coordinates of points. We also characterize the 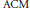$\text{ACM}$ fat point schemes using our description of the eventual behaviour. In fact, in the case that 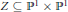$Z\,\subseteq \,{{\mathbb{P}}^{1\,}}\times \,{{\mathbb{P}}^{1}}$ is 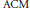$\text{ACM}$, then the entire Hilbert function and its minimal free resolution depend solely on knowing the eventual values of the Hilbert function.