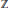A topology on $\mathbb{Z}$, which gives a nice proof that the set of prime integers is infinite, is characterised and examined. It is found to be homeomorphic to 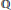$\mathbb{Q}$, with a compact completion homeomorphic to the Cantor set. It has a natural place in a family of topologies on 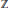$\mathbb{Z}$, which includes the 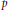$p$-adics, and one in which the set of rational primes $\mathbb{P}$ is dense. Examples from number theory are given, including the primes and squares, Fermat numbers, Fibonacci numbers and $k$-free numbers.

Keywords:

$p$-adic, metrizable, quasi-valuation, topological ring, completion, inverse limit, diophantine equation, prime integers, Fermat numbers, Fibonacci numbers $p$-adic, metrizable, quasi-valuation, topological ring, completion, inverse limit, diophantine equation, prime integers, Fermat numbers, Fibonacci numbers

MSC Classifications:

11B05, 11B25, 11B50, 13J10, 13B35 show english descriptions Density, gaps, topology
Arithmetic progressions [See also 11N13]
Sequences (mod $m$)
Complete rings, completion [See also 13B35]
Completion [See also 13J10] 11B05 - Density, gaps, topology
11B25 - Arithmetic progressions [See also 11N13]
11B50 - Sequences (mod $m$)
13J10 - Complete rings, completion [See also 13B35]
13B35 - Completion [See also 13J10]

top of page | contact us | social media | privacy | site map