Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-17T13:56:37.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Brownian Motion and Harmonic Analysis on Sierpinski Carpets

Published online by Cambridge University Press:  20 November 2018

Martin T. Barlow  and
Richard F. Bass
Martin T. Barlow
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2
Richard F. Bass
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

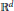We consider a class of fractal subsets of ${{\mathbb{R}}^{d}}$ formed in a manner analogous to the construction of the Sierpinski carpet. We prove a uniform Harnack inequality for positive harmonic functions; study the heat equation, and obtain upper and lower bounds on the heat kernel which are, up to constants, the best possible; construct a locally isotropic diffusion 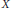$X$ and determine its basic properties; and extend some classical Sobolev and Poincaré inequalities to this setting.

Keywords

60J6060B0560J35Sierpinski carpetfractalHausdorff dimensionspectral dimensionBrownian motionheat equationharmonic functionspotentialsreflecting Brownian motioncouplingHarnack inequalitytransition densitiesfundamental solutions
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 4 , 01 August 1999 , pp. 673 - 744
Copyright
Copyright © Canadian Mathematical Society 1999

References

[AO] Alexander, S. and Orbach, R., Density of states on fractals: “fractons”. J. Physique (Paris) Lett. 43(1982), L625–L631.Google Scholar
[A] Aronson, D. G., Bounds on the fundamental solution of a parabolic equation. Bull. Amer. Math. Soc. 73(1967), 890–896.Google Scholar
[Bar1] Barlow, M. T., Diffusions on fractals. Lectures on Probability Theory and Statistics, École d’ Été de Probabilités de Saint-Flour XXV -1995, 1–121. Lecture Notes in Math. 1690, Springer 1998.Google Scholar
[BB1] Barlow, M. T. and Bass, R. F., The construction of Brownian motion on the Sierpinski carpet. Ann. Inst. H. Poincaré Probab. Statist. 25(1989), 225–257.Google Scholar
[BB2] Barlow, M. T. and Bass, R. F., Local times for Brownian motion on the Sierpinski carpet. Probab. Theory Related Fields 85(1990), 91–104.Google Scholar
[BB3] Barlow, M. T. and Bass, R. F., On the resistance of the Sierpinski carpet. Proc. Roy. Soc. London Ser. A 431(1990), 345–360.Google Scholar
[BB4] Barlow, M. T. and Bass, R. F., Transition densities for Brownian motion on the Sierpinski carpet. Probab. Theory Related Fields 91(1992), 307–330.Google Scholar
[BB5] Barlow, M. T. and Bass, R. F., Coupling and Harnack inequalities for Sierpinski carpets. Bull. Amer. Math. Soc. 29(1993), 208–212.Google Scholar
[BB6] Barlow, M. T. and Bass, R. F., Random walks on graphical Sierpinski carpets. In: Proceedings of the Conference “Random walks and Discrete Potential Theory”, Cortona 1997, to appear.Google Scholar
[BBS] Barlow, M. T., Bass, R. F., and Sherwood, J. D., Resistance and spectral dimension of Sierpinski carpets. J. Phys. A 23(1990), L253–L258.Google Scholar
[BP] Barlow, M. T. and Perkins, E. A., Brownian motion on the Sierpinski gasket. Probab. Theory Related Fields 79(1988), 543–623.Google Scholar
[Bas1] Bass, R. F., Uniqueness for the Skorokhod equation with normal reflection in Lipschitz domains. Electron. J. Probab. (11) 1(1996), 1–29.Google Scholar
[Bas2] Bass, R. F., Probabilistic Techniques in Analysis. Springer, New York, 1995.Google Scholar
[Bas3] Bass, R. F., Diffusions on the Sierpinski carpet. In: Trends in Probability and Related Analysis, World Scientific, Singapore, 1997, 1–34.Google Scholar
[BH] Bass, R. F. and Hsu, P., Some potential theory for reflecting Brownian motion in Hölder and Lipschitz domains. Ann. Probab. 19(1991), 486–508.Google Scholar
[BK] Bass, R. F. and Khoshnevisan, D., Local times on curves and uniform invariance principles. Probab. Theory Related Fields 92(1992), 465–492.Google Scholar
[BAH] Ben-Avraham, D. and Havlin, S., Exact fractals with adjustable fractal and fracton dimensionalities. J. Phys. A. 16(1983), L559–563.Google Scholar
[BST] Ben-Basset, O., Strichartz, R. S. and Teplyaev, A., What is not in the domain of the Laplacian on Sierpinski gasket type fractals? Preprint.Google Scholar
[Ca] Caffarelli, L., Métodos de continuação em equações eliticas não-lineares. Inst. Mat. Pura Apl., Rio de Janeiro, 1986.Google Scholar
[CKS] Carlen, E. A., Kusuoka, S., and Stroock, D. W., Upper bounds for symmetric Markov transition functions. Ann. Inst. H. Poincaré Probab. Statist. 23(1987), 245–287.Google Scholar
[CRRST] Chandra, A. K., Raghavan, P., Ruzzo, W. L., Smolensky, R. and Tiwari, P., The electrical resistance of a graph captures its commute and cover times. Proceedings of the 21st ACM Symposium on theory of computing, 1989.Google Scholar
[Co] Coulhon, T., Dimensioná l’infini d’un semi-groupe analytique. Bull. Sci. Math. 114(1990), 485–500.Google Scholar
[DS] Doyle, P. and Snell, J. L., RandomWalks and Electric Networks. Carus Math. Monographs, Math. Assoc. America, Washington DC, 1984.Google Scholar
[FS] Fabes, E. B. and Stroock, D. W., A new proof of Moser's parabolic Harnack inequality via the old ideas of Nash. Arch. RationalMech. Anal. 96(1986), 327–338.Google Scholar
[FHK] Fitzsimmons, P. J., Hambly, B. M. and Kumagai, T., Transition density estimates for Brownian motion on affine nested fractals. Comm. Math. Phys. 165(1995), 595–620.Google Scholar
[FiS] Fitzsimmons, P. J. and Salisbury, T. S., Capacity and energy for multiparameter Markov processes. Ann. Inst. H. Poincaré Probab. Statist. 25(1989), 325–350.Google Scholar
[Fuk] Fukushima, M., Dirichlet forms, diffusion processes, and spectral dimensions for nested fractals. In: Ideas and methods in stochastic analysis, stochastics and applications, Cambridge University Press, Cambridge, 1992, 151–161.Google Scholar
[FOT] Fukushima, M., Oshima, Y., and Takeda, M., Dirichlet Forms and Symmetric Markov Processes. de Gruyter, Berlin, 1994.Google Scholar
[GAM] Gefen, Y., Aharony, A., and Mandelbrot, B., Phase transitions on fractals: III. Infinitely ramified lattices. J. Phys. A 17(1984), 1277–1289.Google Scholar
[Go] Goldstein, S., Random walks and diffusion on fractals. In: Percolation theory and ergodic theory of infinite particle systems, Springer, New York, 1987, 121–129.Google Scholar
[Gr] Grigor’yan, A. A., The heat equation on noncompact Riemannian manifolds. Math. USSR Sbornik 72(1992), 47–77.Google Scholar
[H1] Hajłasz, P., Sobolev spaces on an arbitrary metric space. Potential Analysis 5(1996), 403–415.Google Scholar
[HHW1] Hattori, K., Hattori, T., and Watanabe, H., Gaussian field theories and the spectral dimensions. Progr. Theoret. Phys. Suppl. 92(1987), 108–143.Google Scholar
[HHW2] Hattori, K., Hattori, T., and Watanabe, H., New approximate renormalisation method on fractals. Phys Rev. A 32(1985), 3730–3733.Google Scholar
[HBA] Havlin, S. and Ben-Avraham, D., Diffusion in disordered media. Adv. in Phys. 36(1987), 695–798.Google Scholar
[Hu] Hutchinson, J. E., Fractals and self-similarity. Indiana J. Math. 30(1981), 713–747.Google Scholar
[Je] Jerison, D., The Poincaré inequality for vector fields satisfying Hörmander conditions. Duke Math. J. 53(1986), 503–523.Google Scholar
[Kig1] Kigami, J., A harmonic calculus on the Sierpinski space. Japan J. Appl. Math. 6(1989), 259–290.Google Scholar
[Kig2] Kigami, J., A harmonic calculus for p.c.f. self-similar sets. Trans. Amer. Math. Soc. 335(1993), 721–755.Google Scholar
[KM] Kinnunen, J. and Martio, O., The Sobolev capacity on metric spaces. Ann. Acad. Sci. Fenn. Math. 21(1996), 367–382.Google Scholar
[Kum1] Kumagai, T., Estimates of the transition densities for Brownianmotion on nested fractals. Probab. Theory Related Fields 96(1993), 205–224.Google Scholar
[Kum2] Kumagai, T., Regularity, closedness, and spectral dimension of the Dirichlet forms on p.c.f. self-similar sets. J. Math. Kyoto Univ. 33(1993), 765–786.Google Scholar
[Kus1] Kusuoka, S., A diffusion process on a fractal. Symposium on Probabilistic Methods in Mathematical Physics, Taniguchi, Katata. Academic Press, Amsterdam, 1987, 251–274.Google Scholar
[Kus2] Kusuoka, S., Diffusion processes on nested fractals. Statistical Mechanics and Fractals. Springer, Berlin, 1993.Google Scholar
[KZ] Kusuoka, S. and Zhou, X. Y., Dirichlet formon fractals: Poincaré constant and resistance. Probab. Theory Related Fields 93(1992), 169–196.Google Scholar
[L] Lindstrøm, T., Brownian motion on nested fractals. Mem. Amer.Math. Soc. 420(1990).Google Scholar
[Lv] Lindvall, T., Lectures on the coupling method. Wiley, New York, 1992.Google Scholar
[LR] Lindvall, T. and Rogers, L. C. G., Coupling of multi-dimensional diffusions by reflection. Ann. Probab. 14(1986), 860–872.Google Scholar
[Man] Mandelbrot, B., The Fractal Geometry of Nature. W. H. Freeman, San Francisco, 1982.Google Scholar
[Ma] Maz’ja, V. G., Sobolev Spaces. Springer, New York, 1985.Google Scholar
[McG] McGillivray, I., Some applications of Dirichlet forms in probability theory. Ph.D. dissertation, Cambridge University, 1992.Google Scholar
[Me] Metz, V., How many diffusions exist on the Vicsek snowflake? Acta Appl. Math. 32(1993), 227–241.Google Scholar
[M] Moser, J., OnHarnack's inequality for elliptic differential equations. Comm. Pure Appl.Math. 14(1961), 577–591.Google Scholar
[Ny] Nyberg, S. O., Brownian motion on simple fractal spaces. Stochastics Stochastics Rep. 55(1995), 21–45.Google Scholar
[O1] Osada, H., Isoperimetric dimension and estimates of heat kernels of pre-Sierpinski carpets. Probab. Theory Related Fields 86(1990), 469–490.Google Scholar
[O2] Osada, H., Personal communication.Google Scholar
[RT] Rammal, R. and Toulouse, G., Random walks on fractal structures and percolation clusters. J. Physique Lettres 44(1983), L13–L22.Google Scholar
[RS-N] Riesz, F. and Nagy, B. Sz.-, Functional Analysis. Ungar, New York, 1955.Google Scholar
[Ro] Rogers, L. C. G., Multiple points of Markov processes in a complete metric space. Séminaire de Probabilités XXIII, Springer, Berlin, 1989, 186–197.Google Scholar
[Sa] Sabot, C., Existence and uniqueness of diffusions on finitely ramified self-similar fractals. Ann. Sci. École Norm. Sup. 30(1997), 605–673.Google Scholar
[SC] Saloff-Coste, L., A note on Poincaré, Sobolev, and Harnack inequalities. Internat. Math. Res. Notices (1992), 27–38.Google Scholar
[Sie] Sierpinski, W., Sur une courbe cantorienne qui contient une image biunivoque et continue de toute courbe donnée. C. R. Acad. Sci. Paris 162(1916), 629–632.Google Scholar
[Tet] Tetali, P., Random walks and the effective resistance of networks. J. Theoret. Probab. 4(1991), 101–109.Google Scholar
[V1] Varopoulos, N. Th., Isoperimetric inequalities and Markov chains. J. Funct. Anal. 63(1985), 215–239.Google Scholar
[V2] Varopoulos, N. Th., Random walks and Brownian motion on manifolds. Sympos. Math. 29(1987), 97–109.Google Scholar
[Z] Zhou, X. Y., On the recurrence of simple random walk on fractals. J. Appl. Probab. 29(1992), 460–466.Google Scholar