Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-25T19:33:13.019Z Has data issue: false hasContentIssue false
  • English
  • Français

Mean Convergence of Lagrange Interpolation for Exponential weights on [-1, 1]

Published online by Cambridge University Press:  20 November 2018

D. S. Lubinsky
D. S. Lubinsky*
Affiliation:
Mathematics Department, Witwatersrand University, Wits 2050, South Africa email: 036dsl@cosmos.wits.ac.za
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We obtain necessary and sufficient conditions for mean convergence of Lagrange interpolation at zeros of orthogonal polynomials for weights on [-1, 1], such as

$$w(x)\,=\,\exp \left( -{{\left( 1-{{x}^{2}} \right)}^{-\alpha }} \right),\,\alpha >0$$

or

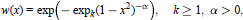$$w(x)=\exp \left( -{{\exp }_{k}}{{\left( 1-{{x}^{2}} \right)}^{-\alpha }} \right),k\ge 1,\alpha >0,$$

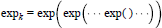where ${{\exp }_{k}}=\exp \left( \exp \left( \cdot \cdot \cdot \exp (\,)\cdot \cdot \cdot \right) \right)$ denotes the $k$-th iterated exponential.

Keywords

41A0542C99
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 6 , 01 December 1998 , pp. 1273 - 1297
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Damelin, S.B., The Weighted Lebesgue Constant of Lagrange Interpolation for Non-Szegö Weights on [-1, 1]. Acta Math. Hungar., to appear.Google Scholar
2. Damelin, S.B., Lagrange Interpolation for non-Szegö Weights on [-1, 1]. Proceedings of the International Workshop on Approximation Theory and Numerical Analysis, to appear.Google Scholar
3. Damelin, S.B. and Lubinsky, D.S., Necessary and Sufficient Conditions for Mean Convergence of Lagrange Interpolation for Erdʺos Weights. Canad. J. Math. 40(1996), 710–736.Google Scholar
4. Damelin, S.B., Necessary and Sufficient Conditions for Mean Convergence of Lagrange Interpolation for Erdʺos Weights II. Canad. J. Math. 40(1996), 737–757.Google Scholar
5. Freud, G., Orthogonal Polynomials. Akademiai Kiado/Pergamon Press, Budapest, 1971.Google Scholar
6. König, H., Vector Valued Lagrange Interpolation and Mean Convergence of Hermite Series. Proc. Essen Conference on Functional Analysis, North Holland.Google Scholar
7. König, H. and Nielsen, N.J., Vector Valued Lp Convergence of Orthogonal Series and Lagrange Interpolation. Math. Forum 6(1994), 183–207.Google Scholar
8. Levin, A.L. and Lubinsky, D.S., Christoffel Functions and Orthogonal Polynomials for Exponential Weights on. [-1, 1]. Mem. Amer.Math. Soc. 535(1994).Google Scholar
9. Lubinsky, D.S., An Extension of the Erdȍs-Turan Inequality for the Sum of Successive Fundamental Polynomials. Ann. of Math. 2(1995), 305–309.Google Scholar
10. Lubinsky, D.S. and D.Matjila, Necessary and Sufficient Conditions for Mean Convergence of Lagrange Interpolation for Freud Weights. SIAM J. Math.Anal. 26(1995), 238–262.Google Scholar
11. Mhaskar, H.N. and Saff, E.B., Where Does The Sup Norm of a Weighted Polynomial Live?. Constr. Approx. 1(1985), 71–91.Google Scholar
12. Mastroianni, G., Boundedness of the Lagrange Operator in Some Functional Spaces. A Survey. to appear.Google Scholar
13. Mastroianni, G. andRusso, M.G.,Weighted Marcinkiewicz Inequalities and Boundedness of the Lagrange Operator. to appear.Google Scholar
14. Muckenhoupt, B., Mean Convergence of Jacobi Series. Proc. Amer.Math. Soc. 23(1970), 306–310.Google Scholar
15. Nevai, P., Orthogonal Polynomials. Mem. Amer.Math. Soc. 213(1979).Google Scholar
16. Nevai, P., Mean Convergence of Lagrange Interpolation II. J. Approx. Theory 30(1980), 263–276.Google Scholar
17. Nevai, P., Mean Convergence of Lagrange Interpolation III. Trans. Amer.Math. Soc. 282(1984), 669–698.Google Scholar
18. Nevai, P., Geza Freud, Orthogonal Polynomials and Christoffel Functions: A Case Study. J. Approx. Theory 48(1986), 3–167.Google Scholar
19. Szabados, J. and Vertesi, P., Interpolation of Functions. World Scientific, Singapore, 1990.Google Scholar
20. Szabados, J., A Survey on Mean Convergence of Interpolatory Processes. J. Comput. Appl. Math. 43(1992), 3–18.Google Scholar