The torsion free Pieri formula

http://dx.doi.org/10.4153/CJM-1998-014-8
Canad. J. Math. 50(1998), 266-289

  Published:1998-04-01
 Printed: Apr 1998

Central to the study of simple infinite dimensional 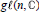$g\ell(n, \Bbb C)$-modules having finite dimensional weight spaces are the torsion free modules. All degree $1$ torsion free modules are known. Torsion free modules of arbitrary degree can be constructed by tensoring torsion free modules of degree $1$ with finite dimensional simple modules. In this paper, the central characters of such a tensor product module are shown to be given by a Pieri-like formula, complete reducibility is established when these central characters are distinct and an example is presented illustrating the existence of a nonsimple indecomposable submodule when these characters are not distinct.